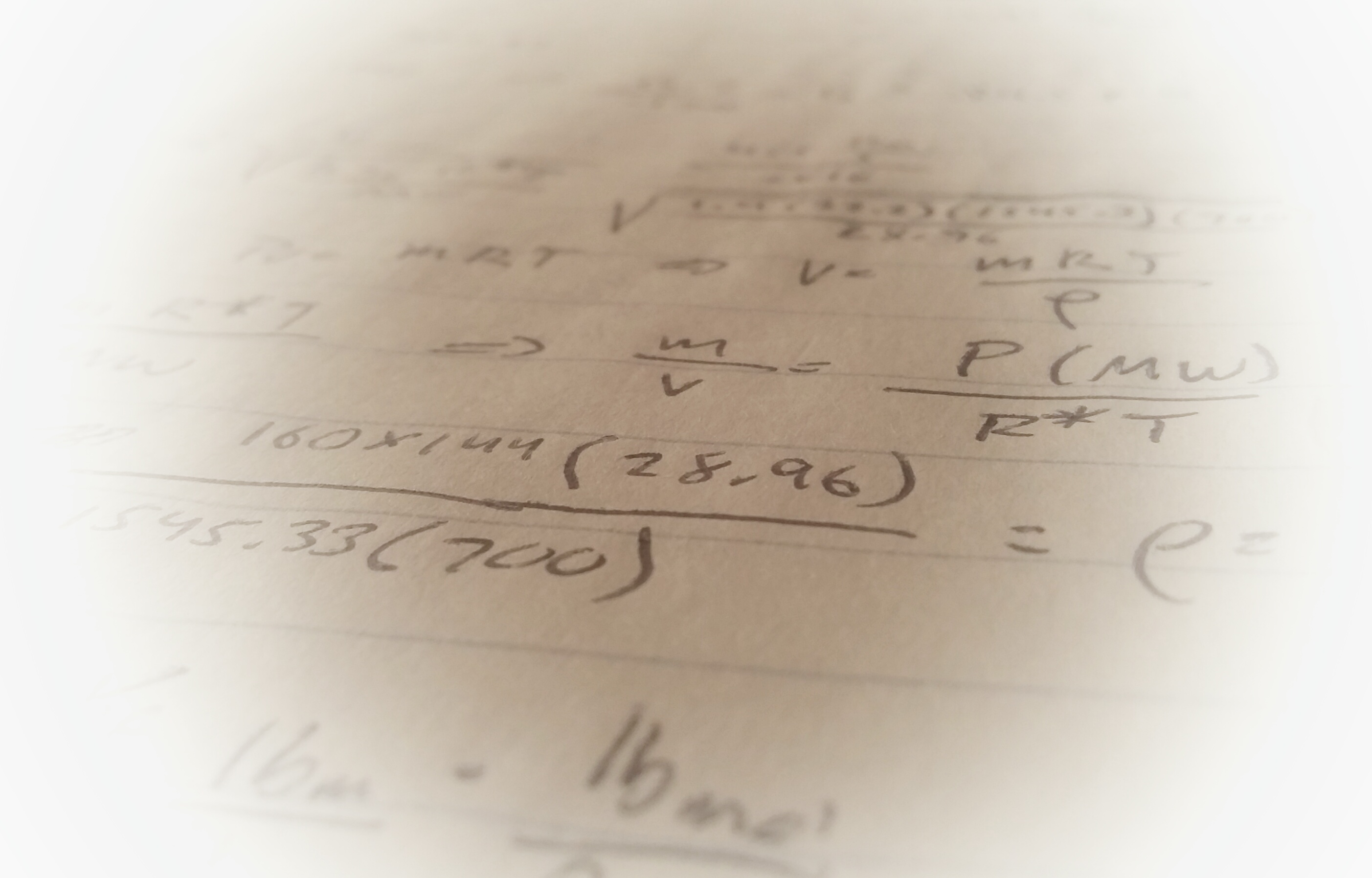
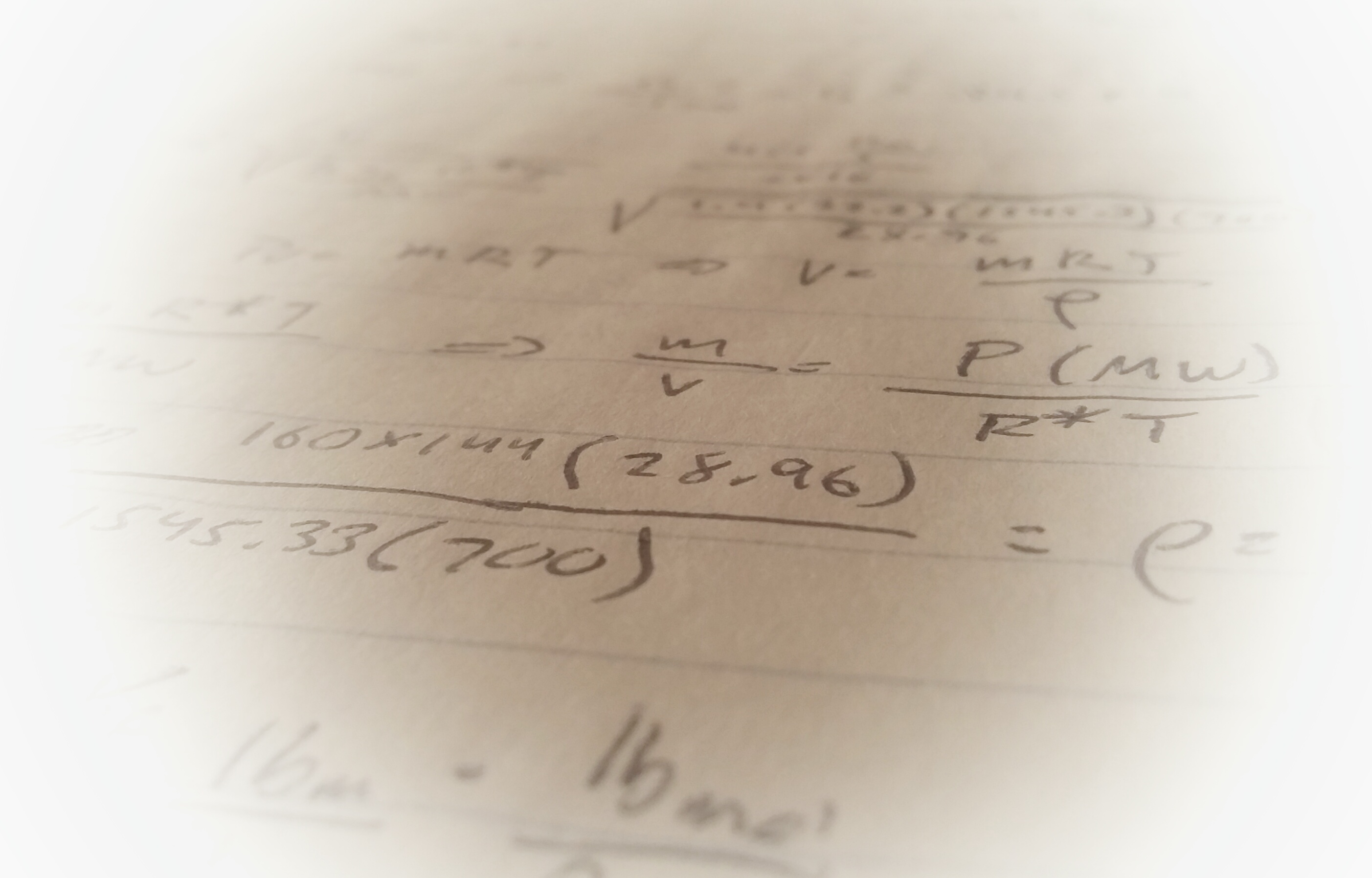
It’s a safe bet to assume thermodynamic cycles of some kind will feature prominently on the PE exam. Whether it be an HVAC or refrigeration problem (vapor compression cycles), a question featuring a steam engine (rankine cycle), or a diesel or gasoline engine (diesel and otto cycles), there are many opportunities to stumble on one of these topics.
Common cycles that may be of use on the exam include the following:
Each of these and how they relate to the PE exam will be discussed in detail.
The Carnot Cycle is an idealized version of a heat engine cycle. As such it operates between two “source and sink” temperatures. Here is the classic schematic of a heat engine style cycle:
A heat engine takes heat from a “hot” source, converts some of that heat energy to work and the rest transfers to the “cold” sink.
It is idealized because a Carnot Cycle is considered fully reversible and adiabatic, i.e. there are not heat losses to account for in the process and the entropy change is considered zero. The P-V and T-S diagrams for this cycle illustrate this point:
The efficiency of a Carnot cycle can be calculated per:
NOTE: This equation requires Tc and Th to be absolute temperature (i.e. Rankine units)
The Carnot Cycle is not so much an actual thermodynamic cycle put to use in real machinery but is more a theoretical benchmark that illustrates the maximum thermal efficiency a so called “heat engine” cycle can achieve. As such, a common use for the Carnot Cycle is in comparison to an actual cycle to determine whether a proposed thermodynamic cycle is realistic. I.e. if the calculated efficiency of a proposed cycle is higher than the corresponding Carnot efficiency, you know the proposed cycle is unrealistic. See Example 1:
An engineer at a steam turbine manufacturer claims some design improvements he is proposing can increase their current thermodynamic cycle design from 50% to 60%. Their current design takes superheated steam at 1150F and produces 5 MW of power after which the steam condenses at 212F. Assuming the steam temperatures won’t change with the proposed design improvements, is the newly proposed efficiency realistic?
A Carnot Cycle represents the absolute maximum efficiency a heat engine cycle can produce. Therefore we can use the given hot and cold temperatures to calculate the theoretical Carnot efficiency:
58% efficiency is the absolute maximum possible with the current conditions, therefore the engineers proposal is unrealistic since it (60%) is higher.
PE exam strategy: Don't forget to use Rankine units for temperature when dealing with Carnot cycle efficiencies. This is a common mistake on the exam!
A Rankine cycle very often represents a steam turbine cycle which is another heat engine style of thermodynamic cycle. Much like the Carnot cycle, a hot source (steam) is passed through a device (steam turbine) to change some of that heat into work, the rest gets passed to the cold sink (condenser). Once the steam condenses, it is pumped back up to a higher temperature and put through a boiler to reheat it back to steam where the process starts again. Below is a schematic of a typical steam turbine or Rankine cycle.
1 to 2: Water is pumped (Win) from the discharge of the condenser at typically saturated liquid conditions to a higher pressure where it enters the boiler.
2 to 3: High pressure enters the boiler where heat is added (Qin) to introduce a phase change from liquid water to steam. The steam can either be saturated or superheated.
3 to 4: Steam from the boiler enters the turbine. Heat energy is extracted and converted to work (Wout) which leaves the system. The working fluid typically leaves as a mixed vapor.
4 to 1: To complete the cycle, the water/vapor mixture enters the condenser where heat is extracted (Qout) from the working fluid and saturated water leaves the condenser.
The diagram for a Rankine cycle is:
For any questions or corrections on this material drop us a line at info@passthepeexam.com